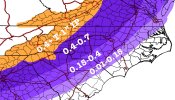
Nice graphic! If there will indeed be a winter storm, I hope to see more of your work!
Well, it's been many of years since an ice storm on that magnitude - something just might give.
_____________________________________________________________________________________________________________________________________________________
As we know, the GFS tonight finally shows a winter storm, which personally I'm not surprised that a winter storm appeared on the model as I've suggested that there could be a winter storm in the near future. I believe the timing is off though with the winter storm - the GFS is indicating that it would come in beginning on the 26th - 4 days later than the last suggested date of the prediction on the 22nd. Of course, we know how the GFS performs in the longer range as it looses resolution and features/timing can be jumbled/inconsistent. As I mentioned on the prediction post last night, the boundary may sag closer towards the southeast before an actual low gets kicked out and that's what I'm going with in terms of the prediction.